What is Ratio?
What is Ratio?
Ratio is a comparison or relation between the quantities of two or more items.
If we know the quantity of one of the items and their ratio, then we can calculate the quantities of the other items in the ratio.
If we know the quantity of one of the items and their ratio, then we can calculate the quantities of the other items in the ratio.
1. I have 5 red cards and 3 green cards.
a) Find the ratio of the number of red cards to the number of green cards.
b) Find the ratio of the number of green cards to the number of red cards.

a) The ratio of the number of red cards to the number of green cards is 5 : 3.
This means that for every 5 red cards there are 3 green cards.
b) The ratio of the number of green cards to the number of red cards is 3 : 5.
This means that for every 3 green cards there are 5 red cards.
Notes:
- The ratio 5 : 3 is read as 5 to 3.
- The numbers 5 and 3 are called the terms of the ratio.
- The ratio 5 : 3 is not the same as the ratio 3 : 5.
2. I have 5 red cards, 3 green cards and 2 blue cards.
a) Find the ratio of the number of red cards to the number of green cards to the number of blue cards.
b) Find the ratio of the number of blue cards to the number of green cards to the number of red cards.

a) The ratio of the number of red cards to the number of green cards to the number of blue cards is 5 : 3 : 2.
This means that for every 5 red cards there are 3 green cards are 2 blue cards.
b) The ratio of the number of blue cards to the number of green cards to the number of red cards is 2 : 3 : 5.
This means that for every 2 blue cards there are 3 green cards and 5 red cards.
This means that for every 5 red cards there are 3 green cards are 2 blue cards.
b) The ratio of the number of blue cards to the number of green cards to the number of red cards is 2 : 3 : 5.
This means that for every 2 blue cards there are 3 green cards and 5 red cards.
3. You need 2 cups of flour and 1 cup of sugar to bake a small cake.
If you use 4 cups of flour to bake a big cake, how many cups of sugar will you need?
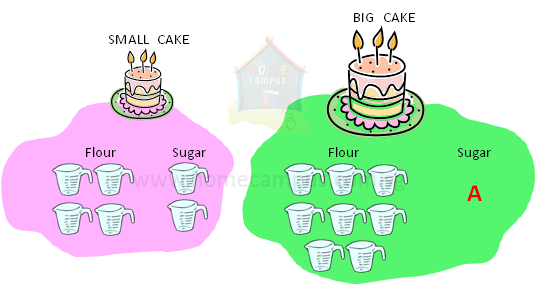
The ratio of flour : sugar is 2 : 1.
Flour : Sugar
= 2 : 1
= (2 : 1) × 2
= 4 : 2 --> big cake
You will need 2 cups of sugar to bake a big cake.
Flour : Sugar
= 2 : 1
= (2 : 1) × 2
= 4 : 2 --> big cake
You will need 2 cups of sugar to bake a big cake.
Whether you bake a small cake or a big one, the ratio of flour : sugar will be 2 : 1.
To bake a big cake, the quantity of flour is doubled. Therefore, the quantity of sugar must also be doubled.
Notes:
- Ratios do not have any unit.
- If you multiply / divide one of the terms of the ratio by a given number then you must also multiply / divide the rest of the terms of the ratio by the same number.