What is Algebra and Algebraic Expressions?
1. What is algebra?
Algebra is the branch of mathematics in which we represent unknown numbers or quantities in terms of letters or symbols.
The unknown number is also called a variable.
The unknown number is also called a variable.
2. How do we write algebraic expressions?
Example: At any time, Pinky had $7 more than Greene.
Let's learn how to write this statement as an algebraic expression.
When Greene had $5, Pinky had $12 as shown below.

When Greene had $57, Pinky had $64 as shown below.

Let's learn how to write this statement as an algebraic expression.
When Greene had $5, Pinky had $12 as shown below.

When Greene had $57, Pinky had $64 as shown below.

When Greene had $x, how much had Pinky?

When Greene had $x, Pinky had $7 more than him.
So, Pinky had $(x + 7).

When Greene had $x, Pinky had $7 more than him.
So, Pinky had $(x + 7).
We use a letter to represent the unknown number.
x is the unknown number here.
x is the unknown number here.
When Greene had $y, Pinky had $(y + 7)?


We can use any letter to represent an unknown number.
We use the letter y to represent the unknown number here.
We use the letter y to represent the unknown number here.
When Pinky had $p, how much had Greene?

When Pinky had $p, Greene had $7 less than her.
So, Greene had $(p − 7).

When Pinky had $p, Greene had $7 less than her.
So, Greene had $(p − 7).
Since Pinky had $7 more than Greene, this means Greene had $7 less than Pinky.
Let's put the above in a table.
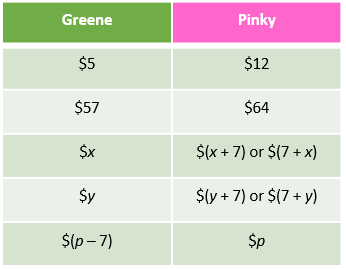
(x + 7), (7 + x), (y + 7), (7 + y) and (p - 7) are all examples of algebraic expressions.
We say that,

(x + 7), (7 + x), (y + 7), (7 + y) and (p - 7) are all examples of algebraic expressions.
We say that,
- (x + 7) and (7 + x) are algebraic expressions in terms of x.
- (y + 7) and (7 + y) are algebraic expressions in terms of y.
- (p - 7) is an algebraic expression in terms of p.
3. Section A has more kids than Section B. There are 37 kids in Section A and x kids in Section B.
a) How many kids are there in Section A and Section B together in terms of x?
b) How many more kids are there in Section A than in Section B expressed in terms of x?
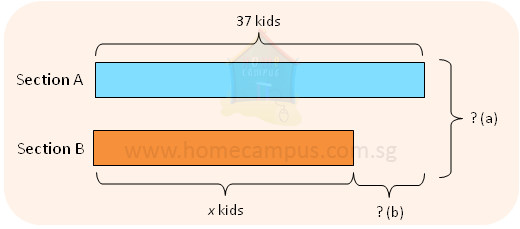
a) Number of kids in Section A = 37
Number of kids in Section B = x
Number of kids in Section A and B together = 37 + x
Number of kids in Section B = x
Number of kids in Section A and B together = 37 + x
b) Number of kids in Section A = 37
Number of kids in Section B = x
The difference between the number of kids in Sections A and B = 37 − x
There are (37 − x) more kids in Section A than in Section B.
Number of kids in Section B = x
The difference between the number of kids in Sections A and B = 37 − x
There are (37 − x) more kids in Section A than in Section B.
4. There are 7 marbles in a bag.
a) How many marbles are there in 3 bags?
b) How many marbles are there in k bags? Write the algebraic expression in terms of k.

There are 7 marbles in 1 bag.
a) There are 7 × 3 or 21 marbles in 3 bags.
a) There are 7 × 3 or 21 marbles in 3 bags.
b) There are 7 × k or 7k marbles in k bags.
We write 7 × k as 7k.
Also, k × 7 = 7k
Also, k × 7 = 7k
5. Sarah had t rolls of ribbon.
She kept 2 rolls for herself and distributed the rest equally among 3 of her cousins.
How many rolls did each cousin get?
Express the answer in terms of t.
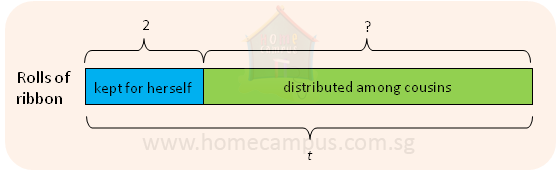
Total number of rolls that Sarah had at first = t
Number of rolls that Sarah kept for herself = 2
Total number of rolls that Sarah distributed among the cousins = (t − 2)
Number of rolls that Sarah kept for herself = 2
Total number of rolls that Sarah distributed among the cousins = (t − 2)
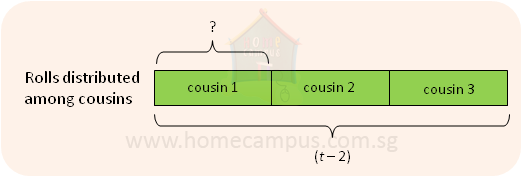
Number of cousins = 3
Number of rolls each cousin got = (t − 2) ÷ 3 =
Number of rolls each cousin got = (t − 2) ÷ 3 =
| t - 2 |
| 3 |
We write (t − 2) ÷ 3 as
or
× (t − 2).
| (t - 2) |
| 3 |
| 1 |
| 3 |