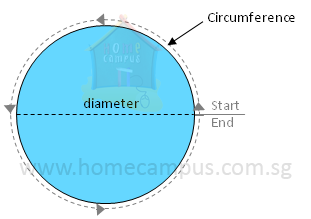
What is the Circumference of a Circle and How to Measure it?
What is the circumference of a circle?
The perimeter of a circle is known as its circumference.
Trace the outline of a few circular objects of different sizes like a CD, a circular bottle lid, a frisbee, a round bowl and a key ring on paper and cut them along their circumference. Then, do the following: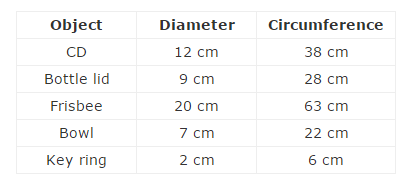
As you will notice, the circumference of each object is about 3 times its diameter.
More precisely, the circumference of a circle is
times its diameter.
The value
is represented by π and read as pi.
The approximate value of π is 3.14.

Trace the outline of a few circular objects of different sizes like a CD, a circular bottle lid, a frisbee, a round bowl and a key ring on paper and cut them along their circumference. Then, do the following:
- Measure the diameter of each circle by folding in half.
- Measure the circumference of each circle using a string.
- Record both readings in a table as below.

As you will notice, the circumference of each object is about 3 times its diameter.
More precisely, the circumference of a circle is
| 22 |
| 7 |
The value
| 22 |
| 7 |
The approximate value of π is 3.14.
What is the formula to calculate circumference of a circle?
Circumference = π × Diameter
Or,
Circumference = π × 2 × Radius = 2 × π × Radius
Or,
Circumference = π × 2 × Radius = 2 × π × Radius
1. Find the circumference of the circles below.
a) 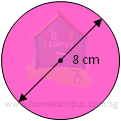
Diameter = 8 cm
Circumference = π × 8 cm = 3.14 × 8 cm = 25.12 cm

Diameter = 8 cm
Circumference = π × 8 cm = 3.14 × 8 cm = 25.12 cm
b) 

Radius = 21 cm
Circumference
= 2 × π × 21 cm
= 2 ×
× 213 cm
= 132 cm
Circumference
= 2 × π × 21 cm
= 2 ×
| 22 |
| 17 |
= 132 cm
When calculation is easy, we use
instead of 3.14 as the value of π
| 22 |
| 7 |
2. Find the perimeters of the following figures.
Round off your answers to 2 decimal places.
a) A semicircle of diameter 17.6 cm.

Perimeter of a semicircle
= Half the circumference of the circle + diameter
= (
× π × 17.6) + 17.6
= (
× 3.14 × 17.6) + 17.6
= 27.632 + 17.6
= 45.232
≈ 45.23 cm

Perimeter of a semicircle
= Half the circumference of the circle + diameter
= (
| 1 |
| 2 |
= (
| 1 |
| 2 |
= 27.632 + 17.6
= 45.232
≈ 45.23 cm
b) A quadrant of radius 5 cm.

Perimeter of a quadrant
= A quarter of the circumference of circle + (2 × radius)
= (
× 21 × 3.14 × 5) + (2 × 5)
= 7.85 + 10
= 17.85 cm

Perimeter of a quadrant
= A quarter of the circumference of circle + (2 × radius)
= (
| 1 |
| 24 |
= 7.85 + 10
= 17.85 cm
c) A three-quarter circle of radius 84 cm.

Perimeter of
circle
=
of the circumference of the circle + (2 × radius)
= (
× 21 ×
× 8412) + (2 × 84)
= (
× 1 ×
× 12) + 168
= 396 + 168
= 564 cm

Perimeter of
| 3 |
| 4 |
=
| 3 |
| 4 |
= (
| 3 |
| 24 |
| 22 |
| 17 |
= (
| 3 |
| 12 |
| 2211 |
| 1 |
= 396 + 168
= 564 cm
3. Can a pizza of radius 12 cm fit into a plate that has a circumference of 100 cm?
Circumference of pizza = 2 × 3.14 × 12 = 75.36 cm
75.36 cm < 100 cm
Yes, the pizza can fit into the plate.
75.36 cm < 100 cm
Yes, the pizza can fit into the plate.
4. The spoke of a wheel is 35 cm long.
How far does the wheel travel in 1 rotation?
Give your answer in metres.

Spoke of the wheel = Radius of the wheel
1 rotation of the wheel
= Circumference of the wheel
= 2 ×
| 22 |
| 17 |
= 220 cm
= 2.2 m
The wheel travels 2.2 m in 1 rotation.