Ratio Word Problems

1. The difference between the capacities of a jar and a bottle is 300 ml.
If the capacities of the bottle and the jar are in the ratio 3 : 5, what is the maximum volume of water in ml that they can hold together?

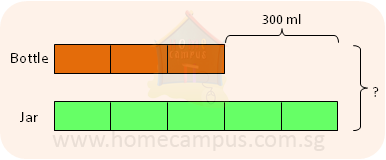
2 units = 300 ml
1 unit = 300 ml ÷ 2 = 150 ml
8 units = 150 ml × 8 = 1200 ml

They can hold 1200 ml of water altogether.

2. The ratio of the breadth of a rectangle to its perimeter is 1 : 8.
Find the area of the rectangle if its length is 45 cm.

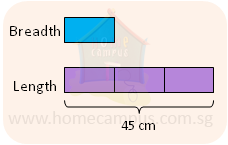
3 units = 45 cm
1 unit = 45 cm ÷ 3 = 15 cm
The breadth of the rectangle is 15 cm.

Area = length × breadth
= 45 cm × 15 cm
= 675 cm²

The area of the rectangle is 675 cm².

Perimeter = 2 × (Length + Breadth)

Length + Breadth = Perimeter ÷ 2

Length = (Perimeter ÷ 2) − Breadth
= (8 units ÷ 2) − 1 unit
= 3 units

3. Sally had $200 at first.
She spent a sum of money on a dress, a necklace and a ring in the ratio 7 : 4 : 5.
If she spent $108 on the jewellery, how much money had she left?

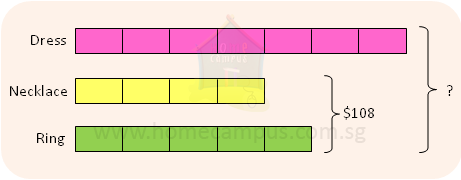
9 units = $108
1 unit = $12
16 units = $12 × 16 = $192
She spent $192 altogether.

$200 − $192 = $8
She had $8 left.

4. The lengths of 3 poles are in the ratio 4 : 5 : 10.
The shortest pole is 48 cm shorter than the longest pole.
What is the length of the poles altogether?

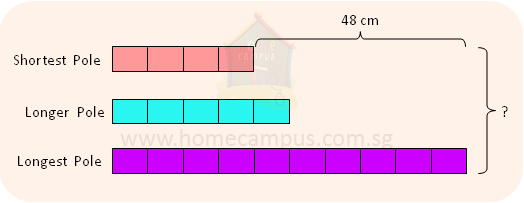
6 units = 48 cm
1 unit = 48 cm ÷ 6 = 8 cm
19 units = 8 cm × 19 = 152 cm

The length of the poles is 152 cm altogether.

5. Pam travelled

1

11

of the distance of her journey by car while the rest by bus and train in the ratio 1 : 4.
If she travelled 532 km more by train than by car, how far did she travel?

1 : 4 = 2 : 8
So,
Bus --> 2 units
Train --> 8 units

8 units − 1 unit = 7 units
She travelled 7 units more by train than by car.

7 units = 532 km
1 unit = 532 km ÷ 7 = 76 km
11 units = 76 km × 11 = 836 km

She travelled 836 km.

6. A pet parrot shop has 322 parrots that are coloured either green or blue or yellow.
The ratio of the number of green parrots to the number of blue parrots is 13 : 4.
The ratio of the number of blue parrots to the number of yellow parrots is 2 : 3.

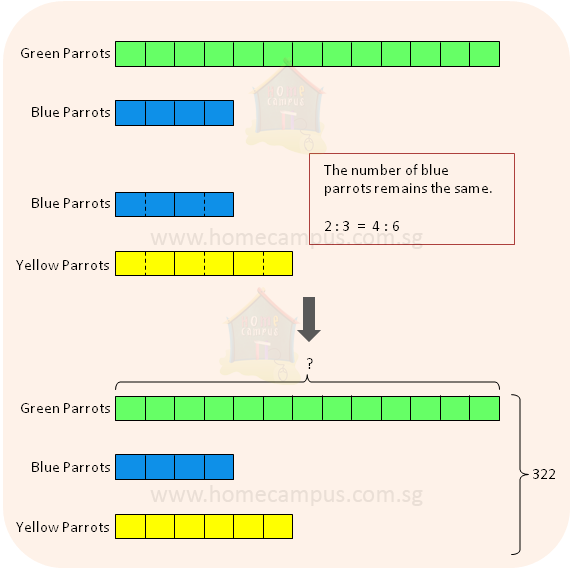
a) Find the ratio of the number of green parrots to the number of blue parrots to the number of yellow parrots.

Number of green parrots : Blue parrots : Yellow parrots
= 13 : 4 : 6

b) Find the number of green parrots.

23 units = 322
1 unit = 322 ÷ 23 = 14
13 units = 14 × 13
= 182

There were 182 green parrots.

7. In a school, for every 5 children born in January there were 3 born in February and for every 2 children born in February there were 5 born in March.

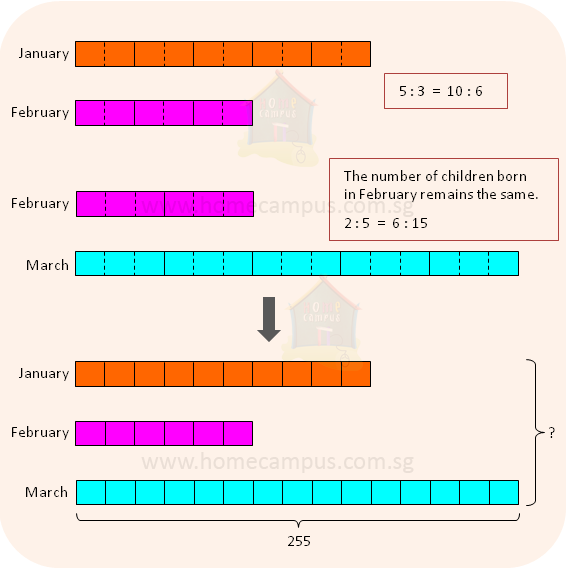
a) What is the ratio of the number of children born in January to the number of children born in March?

Number of children born in January : Born in February
= 5 : 3
= 10 : 6

Number of children born in February : Born in March
= 2 : 5
= 6 : 15

Number of children born in January : Born in March
= 10 : 15
= 2 : 3

b) How many children were born in the three months altogether if 255 of them were born in March?

15 units = 255
1 unit = 255 ÷ 15 = 17
31 units = 17 × 31 = 527

There were 527 children born in the three months altogether.

8. Rayan received twice as much pocket money as Falaq.
After Rayan spent $5 on animal cards, the ratio of Rayan's amount to that of Falaq's became 3 : 2.
Find the amount of pocket money that Falaq received.

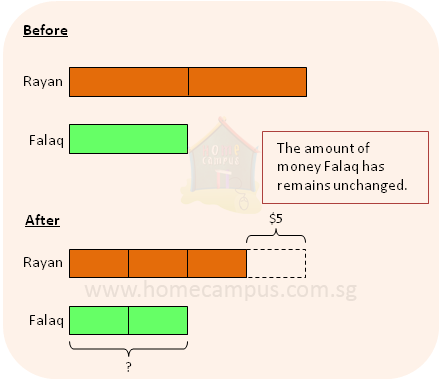
1 unit = $5
2 units = $5 × 2 = $10

Falaq received $10.

9. The ratio of Grace's mass to Laura's mass was 7 : 5 at first.
Then, Laura fell sick and lost

1

10

of her mass.
The new difference between their body masses was 25 kg.

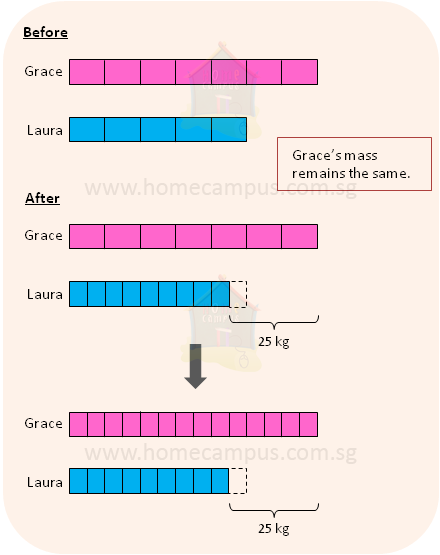
a) Find Grace's mass.

5 units = 25
1 unit = 25 ÷ 5 = 5
14 units = 5 ÷ 14 = 70

Grace's mass was 70 kg.

b) What is the new ratio of Grace's mass to Laura's mass?

Grace's mass : Laura's mass
= 14 : 9

The new ratio of Grace's mass to Laura's mass is 14 : 9.

10. Abby and Nina share a sum of money in the ratio 2 : 3.
Then, Nina gives a sixth of her share to Abby.

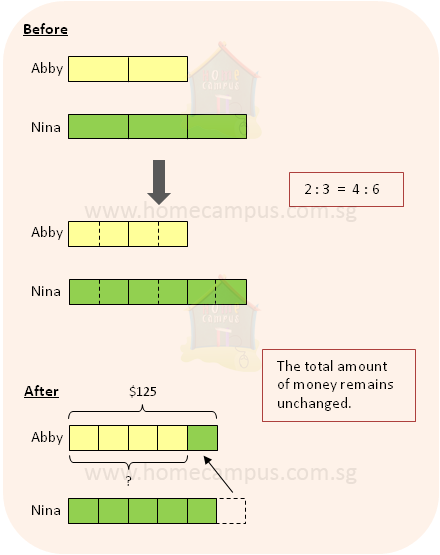
a) Do they now have equal amounts of money?

Abby's amount of money = 5 units
Nina's amount of money = 5 units
5 : 5 = 1 : 1

Yes, they now have equal amounts of money.

b) If Abby now has $125, how much money had she at first?

5 units = $125
1 unit = $125 ÷ 5 = $25
4 units = $25 × 4 = $100

Abby had $100 at first.

11. The ratio of the number of laptops to the number of printers in an electronics store was 2 : 5 at first.
After a shipment of 240 new laptops arrived at the store, there were twice as many laptops as printers.

a) Find the number of printers in the electronics store?

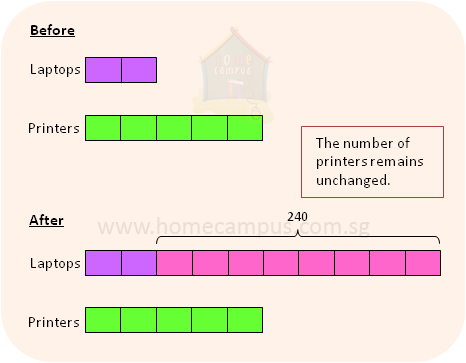
8 units = 240
1 unit = 240 ÷ 8 = 30
5 units = 30 × 5 = 150

There were 150 printers.

b) If a shipment of 120 new printers arrived at the store, what would the ratio of the number of laptops to the number of printers now be?

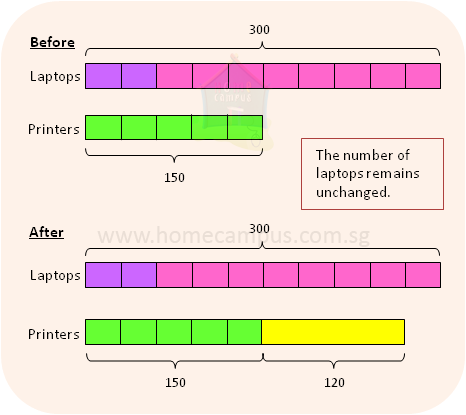
Number of laptops in the store
= 10 units
= 30 × 10
= 300

Number of printer in the store
= 150 + 120
= 270

Number of laptops : printers
= 300 : 270
= 10 : 9

The new ratio would be 10 : 9.

12. Roy, Danny and Henry had a collection of hats.
The ratio of the number of hats that Roy had to the number of hats that Danny had to the number of hats that Henry had was 4 : 5 : 6.
Then, Henry gave

1

4

of his hats to Roy.

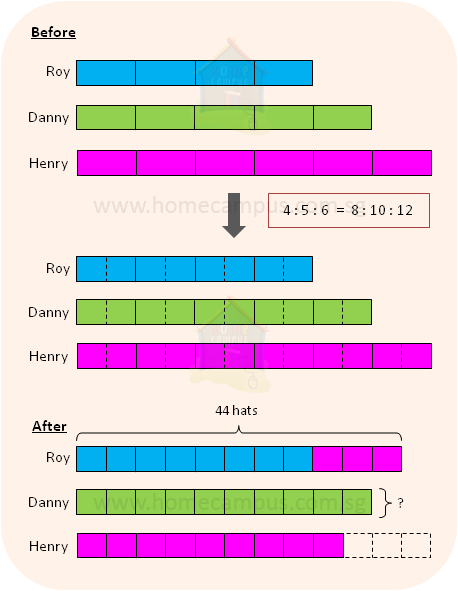
a) What is the new ratio of the number of Roy's hats to that of Danny's to that of Henry's?

Before
Roy's hats : Danny's hats : Henry's hats
= 4 : 5 : 6
= 8 : 10 : 12

After
Roy --> 8 units + 3 units = 11 units
Henry --> 12 units − 3 units = 9 units

The new ratio of Roy's hats : Danny's hats : Henry's hats
= 11 : 10 : 9

b) If Roy now has 44 hats, how many hats has Danny?

11 units = 44
1 unit = 44 ÷ 11 = 4
10 units = 40

Danny has 40 hats.

1. The difference between the capacities of a jar and a bottle is 300 ml. If the capacities of the bottle and the jar are in the ratio 3 : 5, what is the maximum volume of water in ml that they can hold together?

2. The ratio of the breadth of a rectangle to its perimeter is 1 : 8. Find the area of the rectangle if its length is 45 cm.

3. Sally had $200 at first. She spent a sum of money on a dress, a necklace and a ring in the ratio 7 : 4 : 5. If she spent $108 on the jewellery, how much money had she left?

4. The lengths of 3 poles are in the ratio 4 : 5 : 10. The shortest pole is 48 cm shorter than the longest pole. What is the length of the poles altogether?

5. Pam travelled 1 11 of the distance of her journey by car while the rest by bus and train in the ratio 1 : 4. If she travelled 532 km more by train than by car, how far did she travel?

6. A pet parrot shop has 322 parrots that are coloured either green or blue or yellow. The ratio of the number of green parrots to the number of blue parrots is 13 : 4. The ratio of the number of blue parrots to the number of yellow parrots is 2 : 3.