Area and Perimeter - Problem Sums
1. Adriel ran 5 rounds of a square ground of side 70 m.
Find the total distance he ran.

Step 1:
Distance covered in 1 round of the square ground
= Perimeter of the square ground
= 70 + 70 + 70 + 70
= 280 m
Step 2:
Distance covered in 5 rounds of the square ground
= 5 × 280
= 1400 m
He ran a total distance of 1400 m.
Distance covered in 1 round of the square ground
= Perimeter of the square ground
= 70 + 70 + 70 + 70
= 280 m
Step 2:
Distance covered in 5 rounds of the square ground
= 5 × 280
= 1400 m
He ran a total distance of 1400 m.
2. Mrs. Rao gives one rectangular card of sides 18 cm by 14 cm to each of her 7 pupils.
She wants her pupils to glue a ribbon around the border of their own card.
Find the length of the ribbon they will need altogether.

Step 1:
Perimeter of 1 card
= 18 + 14 + 18 + 14
= 64 cm
Step 2:
Each pupil needs 64 cm of ribbon for their card.
Hence, 7 pupils will need
= 7 × 64
= 448 cm
They will need 448 cm of ribbon altogether.
Perimeter of 1 card
= 18 + 14 + 18 + 14
= 64 cm
Step 2:
Each pupil needs 64 cm of ribbon for their card.
Hence, 7 pupils will need
= 7 × 64
= 448 cm
They will need 448 cm of ribbon altogether.
3. Lila has 9 square stamps of side 3 cm each.
She glues them onto an envelope to form a bigger square.
What area of the envelope does the bigger square cover?
The 9 stamps can be arranged to form a square as shown below.

Step 1:
Side of the square formed
= 3 + 3 + 3
= 9 cm
Step 2:
Area of the square formed
= 9 × 9
= 81 cm2
The area of the envelope that the bigger square covers is 81 cm2.
Side of the square formed
= 3 + 3 + 3
= 9 cm
Step 2:
Area of the square formed
= 9 × 9
= 81 cm2
The area of the envelope that the bigger square covers is 81 cm2.
4. Mrs. Bell cuts a 25 cm by 6 cm cloth into 5 equal pieces.
What is the area of each piece?

Step 1:
Area of the cloth
= 25 × 6
= 150 cm2
Step 2:
Area of each cloth
= 150 ÷ 5
= 30 cm2
The area of each piece is 30 cm2.
Area of the cloth
= 25 × 6
= 150 cm2
Step 2:
Area of each cloth
= 150 ÷ 5
= 30 cm2
The area of each piece is 30 cm2.
5. You have 4 squares each of side 8 cm.
Join the squares to form a bigger four-sided figure.
What is the longest possible perimeter that you can get?
Using the 4 squares we can form either a bigger square (Figure A) or a rectangle (Figure B).
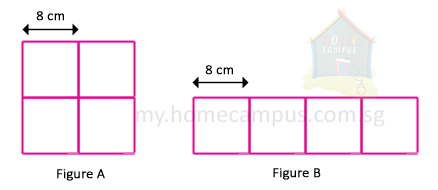
Figure A:
Side of the big square
= Side of the small square + Side of the small square
= 8 + 8
= 16 cm
Perimeter of the big square
= 16 + 16 + 16 + 16
= 64 cm
Figure B:
Length of the rectangle
= 8 + 8 + 8 + 8
= 32 cm
Breadth of the rectangle
= 8 cm
Perimeter of the rectangle
= 32 + 8 + 32 + 8
= 80 cm
Hence, the longest possible perimeter that you can get is 80 cm.
Side of the big square
= Side of the small square + Side of the small square
= 8 + 8
= 16 cm
Perimeter of the big square
= 16 + 16 + 16 + 16
= 64 cm
Figure B:
Length of the rectangle
= 8 + 8 + 8 + 8
= 32 cm
Breadth of the rectangle
= 8 cm
Perimeter of the rectangle
= 32 + 8 + 32 + 8
= 80 cm
Hence, the longest possible perimeter that you can get is 80 cm.