Finding Unknown Angles
ANGLES
This lesson covers the following:
1. Finding the sum of angles on a straight line
Example 1:
Consider a straight line ABC. Draw a line DB on to it meeting it at B.
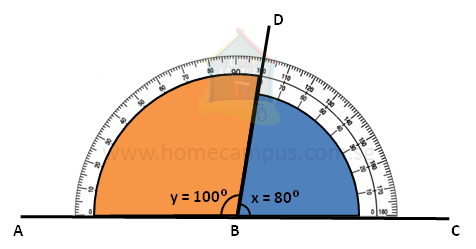
Now, using a protractor, measure ∠x and ∠y.
In the figure above,
∠x = 80°
∠y = 100°
∠x + ∠y = 80° + 100° = 180°

Now, using a protractor, measure ∠x and ∠y.
In the figure above,
∠x = 80°
∠y = 100°
∠x + ∠y = 80° + 100° = 180°
Example 2:
Consider the straight line ABC below. Drop a few lines onto point B and, using a protractor, measure all the angles formed.
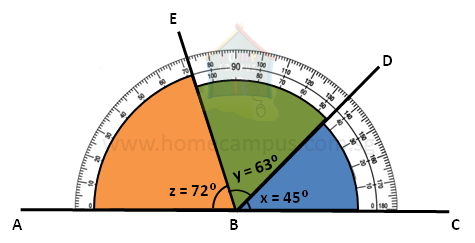
In the figure above, we have dropped 2 lines DB and EB, and the angles formed by them are as follows:
∠x = 45°
∠y = 63°
∠z = 72°
∠x + ∠y + ∠z = 45° + 63° + 72° = 180°

In the figure above, we have dropped 2 lines DB and EB, and the angles formed by them are as follows:
∠x = 45°
∠y = 63°
∠z = 72°
∠x + ∠y + ∠z = 45° + 63° + 72° = 180°
From the examples above it is clear that the sum of angles on a straight line is 180°.
2. Finding the sum of angles at a point
Example 1:
Consider 2 straight lines AB and CD crossing at point O.

We know that,
∠w + ∠x = 180° (sum of angles on a straight line is 180°)
Similarly,
∠y + ∠z is 180° (sum of angles on a straight line is 180°)
Adding all the angles at O, we get,
∠w + ∠x + ∠y + ∠z = 180° + 180° = 360°

We know that,
∠w + ∠x = 180° (sum of angles on a straight line is 180°)
Similarly,
∠y + ∠z is 180° (sum of angles on a straight line is 180°)
Adding all the angles at O, we get,
∠w + ∠x + ∠y + ∠z = 180° + 180° = 360°
Example 2:
Mark a point O and extend a few lines in any direction from it as below.

Now using a protractor measure all the angles at point O. In our case,
∠v = 120°
∠w = 70°
∠x = 20°
∠y = 90°
∠z = 60°
∠v + ∠w + ∠x + ∠y + ∠z = 120° + 70° + 20° + 90° + 60° = 360°

Now using a protractor measure all the angles at point O. In our case,
∠v = 120°
∠w = 70°
∠x = 20°
∠y = 90°
∠z = 60°
∠v + ∠w + ∠x + ∠y + ∠z = 120° + 70° + 20° + 90° + 60° = 360°
From the examples above it is clear that the sum of angles at a point is 360°.
3. Vertically Opposite Angles
Consider 2 straight lines AB and CD crossing each other.


Now, using a protractor measure ∠m, ∠x, ∠n and ∠y.
In our case,
∠m = 120°
∠x = 60°
∠n = 120°
∠y = 60°
In our case,
∠m = 120°
∠x = 60°
∠n = 120°
∠y = 60°
∠m and ∠n form one pair of vertically opposite angles.
∠x and ∠y form a second pair of vertically opposite angles.
∠x and ∠y form a second pair of vertically opposite angles.
What we notice is,
∠m = ∠n , and
∠x = ∠y
Therefore, vertically opposite angles are equal to each other.
∠m = ∠n , and
∠x = ∠y
Therefore, vertically opposite angles are equal to each other.
4. CHALLENGE
Following are 3 straight lines crossing each other at O.

Can you mark the three pairs of vertically opposite angles?
[Help: You may draw similar lines on a piece of paper and use a protractor to measure the angles.]

Can you mark the three pairs of vertically opposite angles?
[Help: You may draw similar lines on a piece of paper and use a protractor to measure the angles.]
Answer:
The 3 pairs of vertically opposite angles are:
The 3 pairs of vertically opposite angles are:
- ∠a and ∠d
- ∠b and ∠e
- ∠c and ∠f