Four-sided Figures: Types and Properties
FOUR-SIDED FIGURES
This lesson covers the following four-sided figures:
1. Rectangles

In a rectangle:
- opposite sides are parallel and equal
- all angles are 90°
2. Squares

In a square:
- all sides are equal
- opposite sides are parallel
- all angles are 90°
3. Parallelograms

In a parallelogram:
- opposite sides are parallel and equal
Rectangles and squares are examples of parallelograms.
4. Rhombuses

In a rhombus:
- all sides are equal
- opposite sides are parallel
A square is an example of a rhombus.
6. Opposite angles of a parallelogram
Make a parallelogram or trapezium using a set square and a ruler, or trace one from your book. Now, measure its angles using a protractor. What do you notice?
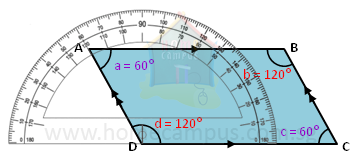
In our case,
∠a = 60°
∠b = 120°
∠c = 60°
∠d = 120°
Therefore,
∠a = ∠c
∠b = ∠d

In our case,
∠a = 60°
∠b = 120°
∠c = 60°
∠d = 120°
Therefore,
∠a = ∠c
∠b = ∠d
Conclusion:
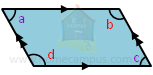

∠a = ∠c
∠b = ∠d
The opposite angles of a parallelogram are equal.
∠b = ∠d
The opposite angles of a parallelogram are equal.

∠a = ∠c
∠b = ∠d
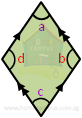
The opposite angles of a rhombus are equal (as a rhombus is a type of parallelogram).
∠b = ∠d
The opposite angles of a rhombus are equal (as a rhombus is a type of parallelogram).
7. Sum of a pair of angles between two parallel lines
Make a parallelogram or trapezium using a set square and a ruler, or trace one from your book. Now, using a protractor, measure all the angles of the figure. What do you notice?
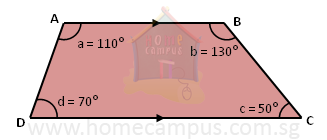
In our case,
∠a = 110°
∠b = 130°
∠c = 50°
∠d = 70°
Therefore,
∠a + ∠d = 110° + 70° = 180°
∠b + ∠c = 130° + 50° = 180°

In our case,
∠a = 110°
∠b = 130°
∠c = 50°
∠d = 70°
Therefore,
∠a + ∠d = 110° + 70° = 180°
∠b + ∠c = 130° + 50° = 180°
Conclusion:
The sum of a pair of angles between two parallel lines is 180°.
The sum of a pair of angles between two parallel lines is 180°.
In a parallelogram,
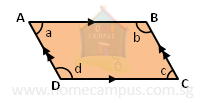

AB // DC
So,
∠a + ∠d = 180°, and ∠b + ∠c = 180°
Also, AD // BC
So,
∠a + ∠b = 180°, and ∠d + ∠c = 180°
So,
∠a + ∠d = 180°, and ∠b + ∠c = 180°
Also, AD // BC
So,
∠a + ∠b = 180°, and ∠d + ∠c = 180°
In a trapezium,
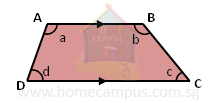

AB // DC
So,
∠a + ∠d = 180°, and ∠b + ∠c = 180°
But, AD// BC
So,
∠a + ∠b ≠ 180°, and ∠d + ∠c ≠ 180°
So,
∠a + ∠d = 180°, and ∠b + ∠c = 180°
But, AD
So,
∠a + ∠b ≠ 180°, and ∠d + ∠c ≠ 180°
