TRIANGLES: Finding Unknown Angles
1. Angles of an isosceles triangle
Make an isosceles triangle as below.
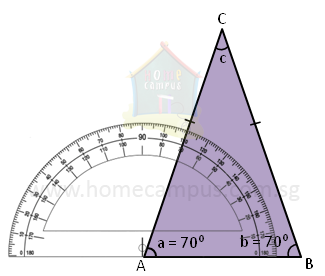
Now, using a protractor, measure the 2 angles opposite its equal sides. What do you notice?
In the figure above,
∠a = 70°
∠b = 70°
The angles opposite the equal sides of the isosceles triangle are equal.

Now, using a protractor, measure the 2 angles opposite its equal sides. What do you notice?
In the figure above,
∠a = 70°
∠b = 70°
The angles opposite the equal sides of the isosceles triangle are equal.
2. Angles of an equilateral triangle
Make an equilateral triangle as below with equal sides.
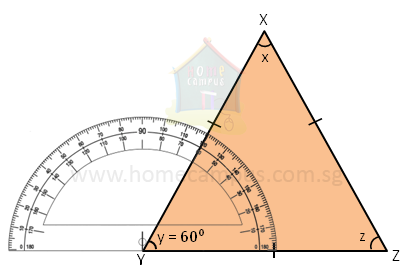
Now, using a protractor, measure all the angles of the triangle. What do you notice?
In the figure above,
∠x = 60°
∠y = 60°
∠z = 60°
All 3 angles of an equilateral triangle are equal. Each angle is 60°.

Now, using a protractor, measure all the angles of the triangle. What do you notice?
In the figure above,
∠x = 60°
∠y = 60°
∠z = 60°
All 3 angles of an equilateral triangle are equal. Each angle is 60°.
3. Angles of a right-angled triangle
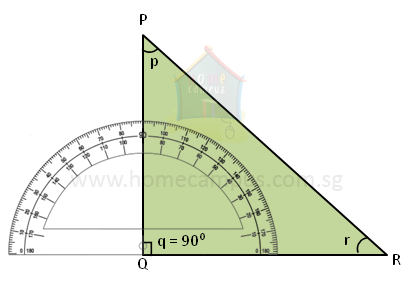
Consider the right-angled triangle above.
∠p + ∠r + ∠q = 180°
∠p + ∠r + 90° = 180°
∠p + ∠r = 90°
The sum of the other two angles of a right-angled triangle is 90°.
4. In the triangle below, AB = BC and ∠ABC = 80°. Find the other two angles.
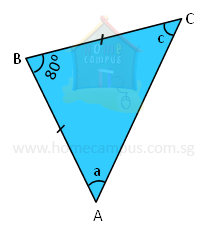
180° − 80° = 100°
100° ÷ 2 = 50°
∠a = 50°
∠c = 50°
100° ÷ 2 = 50°
∠a = 50°
∠c = 50°
The sum of angles of a triangle is 180°.
Since AB = BC, ΔABC is an isosceles triangle.
So, ∠a = ∠c.
So, ∠a = ∠c.
5. In triangle PQR below, PQ = QR and ∠QPR = 45°. Is ΔPQR a right-angled triangle?
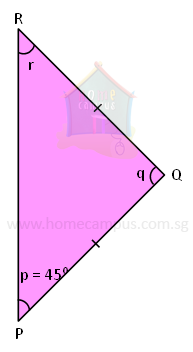
∠p = ∠r
∠r = 45°
∠q = 180° − 45° − 45° = 90°
∠r = 45°
∠q = 180° − 45° − 45° = 90°
Since, PQ = QR, ΔPQR is an isosceles triangle, and ∠p = ∠r.
Since, one of the angles of triangle PQR is 90°, ΔPQR is a right-angled triangle.
It is, in fact, a right-angled isosceles triangle (as one of its angles is 90° and two of its sides are equal).
It is, in fact, a right-angled isosceles triangle (as one of its angles is 90° and two of its sides are equal).