In the figure below,
Area of the rectangle ABCD  =  length  ×  width

Cut the rectangle into 2.
Now, each half is a right-angled triangle.
And, each right-angled triangle, therefore, has half the area of the rectangle.


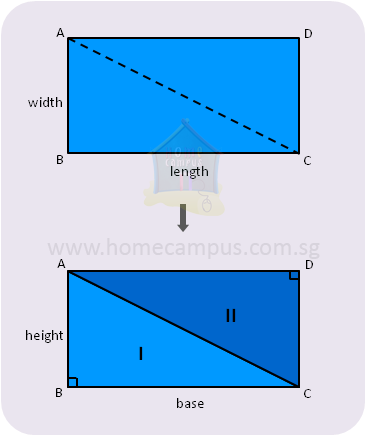
     Area of right-angled triangle
= 

1

2

area of rectangle
= 

1

2

 ×  (length  ×  width)
= 

1

2

 ×  (base  ×  height)

Study the following examples.



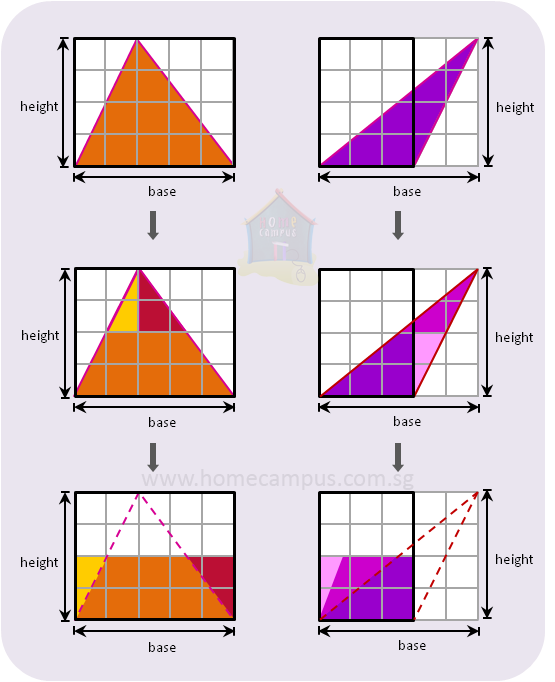
In both examples above, the area of the triangle is half the area of the rectangle made by the base and height.

So,
     Area of a triangle
= 

1

2

of area of rectangle made by the base and height
= 

1

2

 ×  (base  ×  height)

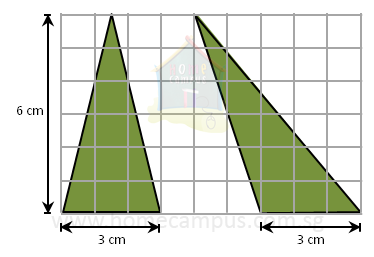
Both triangles above have a base of 3 cm and a height of 6 cm.
Therefore, they both have the same area which is calculated as below:

     Area of triangle
= 

1

2

 ×  (base  ×  height)
= 

1

2

 ×  3 cm  ×  6 cm
=   9 cm²

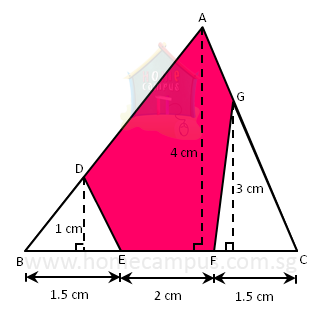
     Area of triangle ABC
= 

1

2

 ×  (1.5 cm  +  2 cm  +  1.5 cm)  ×  4 cm
= 

1

2

 ×  5 cm  ×  4 cm
=   10 cm²

     Area of triangle BED
= 

1

2

 ×  1.5 cm  ×  1 cm
=   0.75 cm²

     Area of triangle GFC
= 

1

2

 ×  1.5 cm  ×  3 cm
=   2.25 cm²

     Area of pentagon ADEFG
=   Area (ABC) −  Area (BED)  −  Area (GFC)
=   10 cm²  −  0.75 cm²  −  2.25 cm²
=   7 cm²