Simplifying and Evaluating Algebraic Expressions
1. There are p pencils in one box. Rayan has 6 boxes of pencils and Amelia has 4 boxes of pencils.
a) How many pencils do they have altogether in terms of p?
b) How many more pencils has Rayan than Amelia in terms of p?
c) If each box has 6 pencils, how many more pencils has Rayan than Amelia?

a) Rayan has 6 boxes of pencils. Each box has p pencils.
p + p + p + p + p + p = 6 × p = 6p
Rayan has 6p pencils.
Amelia has 4 boxes of pencils. Each box has p pencils.
p + p + p + p = 4 × p = 4p
Amelia has 4p pencils.
6p + 4p = 10p
They have 10p pencils altogether.
p + p + p + p + p + p = 6 × p = 6p
Rayan has 6p pencils.
Amelia has 4 boxes of pencils. Each box has p pencils.
p + p + p + p = 4 × p = 4p
Amelia has 4p pencils.
6p + 4p = 10p
They have 10p pencils altogether.
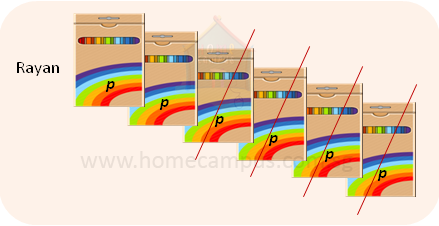
b) 6p − 4p = 2p
Rayan has 2p more pencils than Amelia.
Rayan has 2p more pencils than Amelia.
c) 2p = 2 × p = 2 × 6 = 12
Rayan has 12 more pencils than Amelia.
Rayan has 12 more pencils than Amelia.
The value of p = 6
2. Simplify the following expressions.
a) 5m + m = ?
Let m be the number of marbles in each bag.

5m + m = 6m

5m + m = 6m
b) 5m − 2m = ?
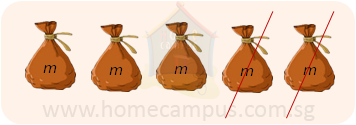
5m − 2m = 3m

5m − 2m = 3m
c) 5m − 3m + 2m = ?
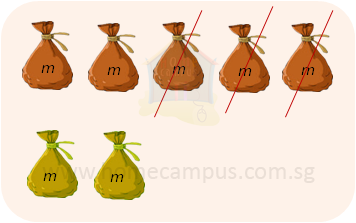
5m − 3m + 2m = 2m + 2m = 4m

5m − 3m + 2m = 2m + 2m = 4m
d) 5m + 6 − 2m − 3 = ?
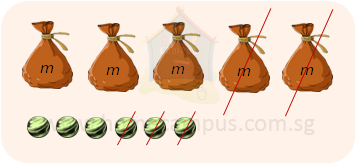

5m + 6 − 2m − 3 = 5m − 2m + 6 − 3 = 3m + 3
5m − 2m = 3m
6 − 3 = 3
6 − 3 = 3
3. Find the value of each of the expressions below when b = 4.
a) 5b − 2b + 2
= 3b + 2 (Simplify)
= (3 × b) + 2
= (3 × 4) + 2 (Put the value of b as 4)
= 12 + 2
= 14
= 3b + 2 (Simplify)
= (3 × b) + 2
= (3 × 4) + 2 (Put the value of b as 4)
= 12 + 2
= 14
b)
=
=
=
= 7
| 8b + 3 |
| 5 |
=
| (8 x 4) + 3 |
| 5 |
=
| 32 + 3 |
| 5 |
=
| 35 |
| 5 |
= 7
4. Jane has t stamps. Jill has 3 times as many stamps as Jane and Julia has 2 stamps more than Jane.
a) Express the number of stamps that they have altogether in terms of t.
b) How many more stamps has Jill than Julia if Jane has 8 stamps?
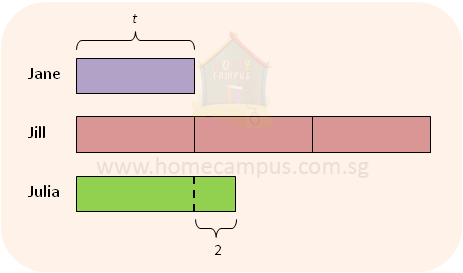
a) Jane has t stamps.
Jill has 3 × t stamps or 3t stamps.
Julia has t + 2 stamps.
Total stamps = t + 3t + t + 2 = 5t + 2
b) 3t − t − 2 = 2t − 2
Jill has 2t − 2 more stamps than Julia.
Now, replace t by 8.
2t − 2 = 2 × 8 − 2 = 14
Jill has 14 more stamps than Julia.
Jill has 2t − 2 more stamps than Julia.
Now, replace t by 8.
2t − 2 = 2 × 8 − 2 = 14
Jill has 14 more stamps than Julia.
5. A zoo has 3 times as many terrestrial animals as aquatic animals and 122 more aquatic animals than amphibians.
a) Write an algebraic expression to express the total number of animals in the zoo in terms of the number of aquatic animals.
b) If there are 1633 animals in the zoo altogether, how many terrestrial animals are there?
a) To express the total number of animals in terms of the number of aquatic animals, we assume the number of aquatic animals to be k.
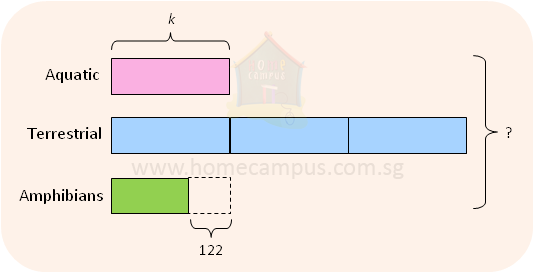
Number of aquatic animals = k
Number of terrestrial animals = 3k
Number of amphibians = k − 122
Total number of animals = k + 3k + k − 122 = 5k − 122
Total number of animals in the zoo is 5k − 122 where k is the number of aquatic animals.

Number of aquatic animals = k
Number of terrestrial animals = 3k
Number of amphibians = k − 122
Total number of animals = k + 3k + k − 122 = 5k − 122
Total number of animals in the zoo is 5k − 122 where k is the number of aquatic animals.
b) 5k − 122 = 1633
5k = 1633 + 122 = 1755
k = 1755 ÷ 5 = 351
3k = 3 × 351 = 1053
There are 1053 terrestrial animals in the zoo.
5k = 1633 + 122 = 1755
k = 1755 ÷ 5 = 351
3k = 3 × 351 = 1053
There are 1053 terrestrial animals in the zoo.
6. A memory card costs $69. A digital camera costs $16y more than the memory card. A tripod stand costs $y less than the memory card.
a) If Eric bought all the three items, how much did he pay? Express your answer in terms of y.
b) If the tripod stand cost $39, find the cost of the camera.
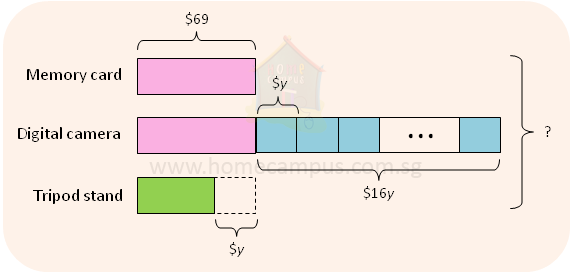
a) Cost of memory card = $69
Cost of digital camera = $69 + $16y
Cost of tripod stand = $69 − $y
Total cost of all items = $69 + $69 + $16y + $69 − $y = $207 + $15y
Eric paid $207 + $16y for all the three items.
b) Cost of tripod stand = $69 − $y = $39
y = 30
Cost of camera = $69 + $16y
= $69 + ($16 × y)
= $69 + ($16 × 30)
= $69 + $480
= $549
The cost of the camera is $549.
y = 30
Cost of camera = $69 + $16y
= $69 + ($16 × y)
= $69 + ($16 × 30)
= $69 + $480
= $549
The cost of the camera is $549.
7. A bag of chips has a mass of q grams and a box of cookies has twice as much mass.
a) What is the mass of a box of cookies in terms of q?
b) Nur bought 3 bags of chips and some boxes of cookies. The total mass of the items she bought was 1.8 kg. What was the mass of cookies that she bought expressed in terms of q?
c) If each bag of chips had a mass of 120 grams, how many boxes of cookies did she buy?
a) 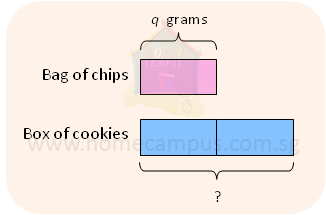
The mass of a box of cookies is 2q grams.

The mass of a box of cookies is 2q grams.
b) 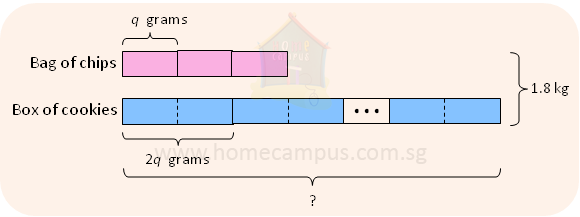
Total mass of items = 1.8 kg = 1800 grams
Mass of 3 bags of chips = 3 × q grams = 3q grams
Mass of all the boxes of cookies = (1800 − 3q) grams

Total mass of items = 1.8 kg = 1800 grams
Mass of 3 bags of chips = 3 × q grams = 3q grams
Mass of all the boxes of cookies = (1800 − 3q) grams
c) Mass of 1 box of cookies = 2q grams
= 2 × 120
= 240 grams
Mass of all the boxes of cookies = (1800 − 3q) grams
= (1800 − 3 × 120) grams
= (1800 − 360) grams
= 1440 grams
Total number of boxes of cookies = 1440 ÷ 240 = 6
Nur bought 6 boxes of cookies.
= 2 × 120
= 240 grams
Mass of all the boxes of cookies = (1800 − 3q) grams
= (1800 − 3 × 120) grams
= (1800 − 360) grams
= 1440 grams
Total number of boxes of cookies = 1440 ÷ 240 = 6
Nur bought 6 boxes of cookies.