Pie Charts: Word Problems
Word Problem 1. A community centre organized a racial harmony fair through which it collected a sum of $5880. The pie chart below shows the amount of money collected by the various stalls.
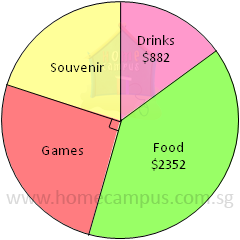
a) Find the sum of money collected by the games stall.
× $5880 = $1470
The games stall collected $1470.
| 1 |
| 4 |
The games stall collected $1470.
b) What percentage of the total money was collected by the souvenir stall?
$5880 − $882 − $2352 − $1470 = $1176
The souvenir stall collected $1176.
× 100% = 20%
The souvenir stall collected 20% of the total money.
$5880 − $882 − $2352 − $1470 = $1176
The souvenir stall collected $1176.
| $1176 |
| $5880 |
The souvenir stall collected 20% of the total money.
c) What fraction of the total money was collected by the foods stall?
=
of the total money was collected by the foods stall.
| $2352 |
| $5880 |
| 2 |
| 5 |
| 2 |
| 5 |
d) What fraction of the total money was collected by the drinks stall?
=
of the total money was collected by the drinks stall.
| $882 |
| $5880 |
| 3 |
| 20 |
| 3 |
| 20 |
e) What percentage of the total money was collected by the food and drinks stalls?
$2352 + $882 = $3234
The food and drinks stalls collected $3234 together.
× 100% = 55%
55% of the total money was collected by the food and drinks stalls.
$2352 + $882 = $3234
The food and drinks stalls collected $3234 together.
| $3234 |
| $5880 |
55% of the total money was collected by the food and drinks stalls.
f) What was the ratio of the sum of money collected by the food and drinks stalls to the sum of money collected by the games stall?
$3234 : $1470 = 11 : 5
The ratio of of the sum of money collected by the food and drinks stalls to the sum of money collected by the games stall was 11 : 5.
$3234 : $1470 = 11 : 5
The ratio of of the sum of money collected by the food and drinks stalls to the sum of money collected by the games stall was 11 : 5.
Word Problem 2. A clothing merchant has 3840 pieces of clothing of 5 types. The pie chart below represents what fraction of the clothing are of each type. PQ is the diameter of the circle on the pie chart.
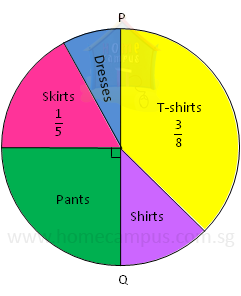
a) How many shirts does the clothing merchant have?
−
=
=
× 3840 = 480
The clothing merchant has 480 shirts.
| 1 |
| 2 |
| 3 |
| 8 |
| 4 - 3 |
| 8 |
=
| 1 |
| 8 |
| 1 |
| 8 |
The clothing merchant has 480 shirts.
b) What fraction of the clothing are dresses?
−
−
=
=
of the clothing are dresses.
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 4 |
| 10 - 2 - 5 |
| 20 |
=
| 3 |
| 20 |
| 3 |
| 20 |
c) How many dresses are there?
× 3840 = 576
There are 576 dresses.
| 3 |
| 20 |
There are 576 dresses.
d) Are there more dresses or skirts? How many more?
From the pie chart it is clear that there are more skirts than dresses (as the pie representing the skirts is bigger than the pie representing the dresses).
× 3840 = 768
There are 768 skirts.
768 − 576 = 192
There are 192 more skirts than dresses.
From the pie chart it is clear that there are more skirts than dresses (as the pie representing the skirts is bigger than the pie representing the dresses).
| 1 |
| 5 |
There are 768 skirts.
768 − 576 = 192
There are 192 more skirts than dresses.
e) What is the ratio of the number of T-shirts to the number of shirts?
× 3840 = 1440
There are 1440 T-shirts.
1440 : 480 = 3 : 1
The ratio of the number of T-shirts to the number of shirts is 3 : 1.
| 3 |
| 8 |
There are 1440 T-shirts.
1440 : 480 = 3 : 1
The ratio of the number of T-shirts to the number of shirts is 3 : 1.
f) How many percent of the clothing are pants and skirts?
× 3840 = 960
There are 960 pairs of pants.
960 + 768 = 1728
There are 1728 pants and skirts together.
× 100 = 45%
45% of the clothing are pants and skirts.
| 1 |
| 4 |
There are 960 pairs of pants.
960 + 768 = 1728
There are 1728 pants and skirts together.
| 1728 |
| 3840 |
45% of the clothing are pants and skirts.
Word Problem 3. A florist has some roses in 5 different colours. The pie chart below shows what percentage of the roses are in each colour. AB is a diameter of the circle on the pie chart.
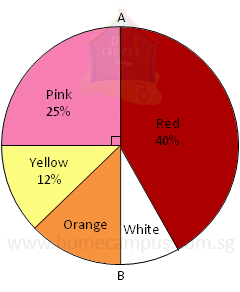
a) How many percent of the roses are orange?
50% − 25% − 12% = 13%
13% of the roses are orange.
50% − 25% − 12% = 13%
13% of the roses are orange.
b) Given that there are 36 yellow roses, how many roses are there altogether?
12% --> 36
1% --> frGen(36,12)
= 3
100% --> 3 × 100
= 300
There are 300 roses altogether.
12% --> 36
1% --> frGen(36,12)
= 3
100% --> 3 × 100
= 300
There are 300 roses altogether.
c) What is the ratio of the number of white roses to the number of red roses?
50% − 40% = 10%
10% of the roses are white.
× 300 = 30
There are 30 white roses.
40% of the roses are red.
× 300 = 120
There are 120 red roses.
30 : 120 = 1 : 4
The ratio of the number of white roses to the number of red roses is 1 : 4.
50% − 40% = 10%
10% of the roses are white.
| 10 |
| 100 |
There are 30 white roses.
40% of the roses are red.
| 40 |
| 100 |
There are 120 red roses.
30 : 120 = 1 : 4
The ratio of the number of white roses to the number of red roses is 1 : 4.