Equivalent Fractions and Ratios

Practice Unlimited Questions

1. Leela adds fertilizer to her flower pots which are all of the same size.
She uses 3 tablespoons of fertilizer for every 9 flower pots.

a)   Express the number of tablepoons of fertilizer as a fraction of the number of flower pots in the simplest form.
3
9
 = 
1
3
b)   If she has 6 flower pots, how many tablespoons of fertilizer does she need?
1
3
 = 
?
6

1
3
 = 
1 x 2
3 x 2
 = 
2
6


She needs 2 tablespoons of fertilizer.
c)   How many flower pots are needed if 5 tablespoons of fertilizer is used?
1
3
 = 
1 x 5
3 x 5
 = 
5
15


15 flower pots are needed if 5 tablespoons of fertilizer are used.

2. Larry is making a pattern with 14 green tiles for every 70 blue tiles.

a)   Find the ratio of the number of green tiles to the number of blue tiles in the simplest form.
14 : 70  =  7 : 35  =  1 : 5

The ratio of the number of green tiles to the number of blue tiles is 1 : 5.
b)   Find the ratio of the number of blue tiles to the number of green tiles.
70 : 14  =  35 : 7  =  5 : 1

The ratio of the number of blue tiles to the number of green tiles is 5 : 1.
c)   If he uses 35 green tiles, how many blue tiles does he use?
The number of green tiles and blue tiles used are in the ratio 1 : 5.

ratio and fraction
1 unit   =  35
5 units  =  35  ×  5  =  175

He uses 175 blue tiles.
d)   If he uses a total of 120 tiles, how many of them are blue?
Again, the ratio of the number of green tiles to the number of blue tiles is 1 : 5.

ratio and fraction
6 units  =  120
1 unit   =  120  ÷  6  =  20
6 units  =  20  ×  5  =  100

There are 100 blue tiles.
e)   He adds red tiles to the pattern so the ratio of the number of green tiles to the number of blue tiles to the number of red tiles is 1:5:2. If he uses 240 tiles altogether, how many of them are red?
The ratio of the number of green tiles to the blue tiles to red tiles is 1 : 5 : 2.

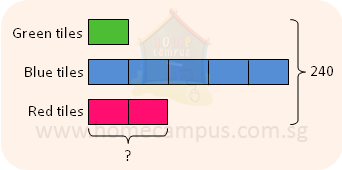
ratio and fraction
8 units  =  240
1 unit   =  240  ÷  8  =  30
2 units  =  30  ×  2  =  60

There are 60 red tiles.