Quadrilaterals: Rectangles and Squares

Practice Unlimited Questions

1. Properties of Rectangles and Squares

A geometrical figure with 4 sides is a quadrilateral.
Rectangles and squares are quadrilaterals.


In a rectangle,
  • Opposite sides are equal and parallel
  • All angles are right angles (90°)



In a square,
  • All sides are equal
  • Opposite sides are parallel
  • All angles are right angles (90°)


Fun Fact: All Squares are Rectangles. Can you prove it? Hint: Check the properties above.

2. Which of the following quadrilaterals are squares or rectangles and which are not?

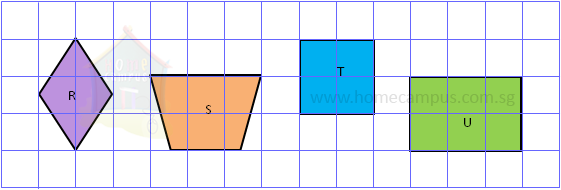
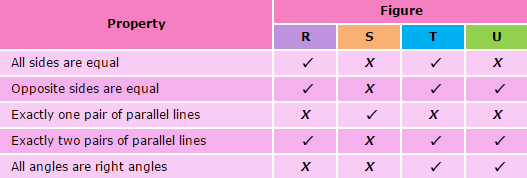
square metre or square meter
square metre or square meter
Figure T is a square.
Figure U is a rectangle.

3. Following quadrilaterals are squares or rectangles.
In each figure, find the lengths of the unknown sides.

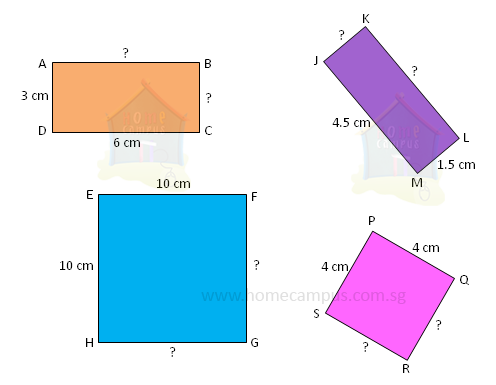
square metre or square meter
ABCD is a rectangle.
AB = 6 cm
BC = 3 cm
Opposite sides of a rectangle are equal.
EFGH is a square.
FG = 10 cm
GH = 10 cm
All sides of a square are equal.
JKLM is a rectangle.
JK = 1.5 cm
KL = 4.5 cm

PQRS is a square.
QR = 4 cm
RS = 4 cm

4. In the figures below, ABCD is a square and PQRS is a rectangle.
Find the unknown marked angles a and b.

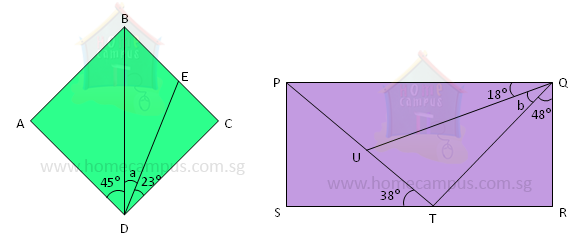
square metre or square meter
In Square ABCD,
∠ADC  =  90°
45° + ∠a + 23°  =  90°
∠a  =  90° − 45° − 23°
=  22°

In Rectangle PQRS,
∠PQR  =  90°
18° + ∠b + 48°  =  90°
∠b  =  90° − 18° − 48°
=  24°

5. The figure below is made of a rectangle ABCD and a square EFGH.
Find the length of BC.

square metre or square meter
In Square EFGH,
EF  =  7 cm  −  2 cm
=  5 cm
GF  =  EF  =  5 cm
BC  =  3 cm  +  GF  +  2 cm
=  3 cm  +  5 cm  +  2 cm
=  10 cm
All sides of a square are equal.

6. All lines in the figure below meet at right angles.
Find the lengths of AB, EF and AL.

square metre or square meter
AB  =  12 cm  +  50 cm
=  62 cm

EF  =  50 cm  −  25 cm
=  25 cm

AL  =  14 cm  +  14 cm  +  14 cm  +  14 cm  +  14 cm
=  70 cm