What are like fractions?

Like fractions are two or more fractions that have the same denominator.

Example:

1 5

and

2 5

(both these fractions have the same denominator of 5)

What are unlike fractions?

Unlike fractions are two or more fractions that do not have the same denominator.

Example:

1 3

and

1 4

(the denominators of these two fractions are different)

How do you compare unlike fractions?

Example:

Compare

1 3

and

1 4

.

Let's use lasagnas to mark these two fractions. Since the given fractions have unlike denominators, we cannot mark them on a single lasagna. Let's use two lasagnas instead.

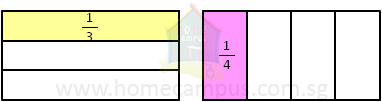But it is not clear which of the two fractions is greater. In order to compare the two fractions, we must first change them to like fractions. Here are the steps to change unlike fractions to like fractions:

Step 1:

Find the product of 3 and 4 (the two denominators).
      3 × 4 = 12

Step 2:

Change each of the two fractions to its equivalent fraction so that the new denominator is 12.

1 3	=	? 12	=>	1 × 4 3 × 4	=	4 12
1 4	=	? 12	=>	1 × 3 4 × 3	=	3 12

Here's how to mark the two fractions on a single lasagna:

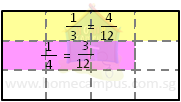Step 3:

It is clear now that

4 12

, which is the equivalent of

1 3

is greater than

3 12

which is the equivalent of

1 4

.

Therefore,

1 3

is greater than

1 4

.

Compare

1 6

and

1 4

.

Step 1:

Find the product of 6 and 4 = 24

Step 2:

Change each of the two unlike fractions to its equivalent so that the new denominator is 24.

1 6	=	? 24	=>	1 × 4 6 × 4	=	4 24
1 4	=	? 24	=>	1 × 6 4 × 6	=	6 24

Here's how the two fractions look like on a lasagna:

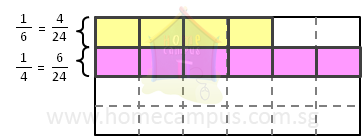
Step 3:

It is clear now that

6 24

or

1 4

is greater than

4 24

or

1 6

.

What is LCM or Least Common Multiple?

While the above method of converting unlike fractions to like fractions works, it is not the best method especially when dealing with more than two numbers or with bigger numbers. There is a better method to do so and it is called LCM or least common multiple.

Example:

Find the LCM of 6 and 4.

Here are the steps to find the LCM of 6 and 4.

Step 1:

Find the multiples of 6 and the multiples of 4.
6 => 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, ...
4 => 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, ...

Step 2:

Find the common multiples of 6 and 4.
They are: 12, 24, 36, ...

Step 3:

Find the least (or smallest) of the common multiples of 6 and 4.
It is 12.
So, the LCM of 6 and 4 is 12.

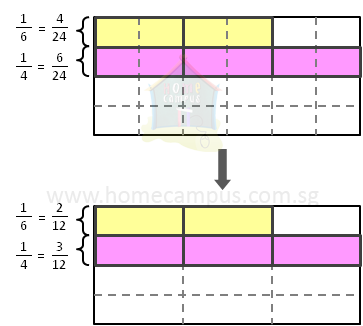
Compare

1 6

and

1 4

using LCM.

LCM or least common multiple, as we mentioned above, is a way to find out a new common denominator for the given unlike fractions so they can be changed to like fractions.

Here are the steps to compare the given unlike fractions:

Step 1:

Take the two unlike denominators, 6 and 4, and find a new common denominator using LCM.

Step 2:

We know from above that the LCM of 6 and 4 = 12.

Step 3:

Change the two unlike fractions so each has a denominator of 12.

1 6	=	? 12	=>	1 × 2 6 × 2	=	2 12
1 4	=	? 12	=>	1 × 3 4 × 3	=	3 12

This tells us we need not cut the lasagna into 24 pieces (6 × 4). It is sufficient enough to cut the lasagna into 12 pieces and still be able

to mark the unlike fractions

1 6

and

1 4

on it for comparison.