Measurement: Volume of Cubes and Cuboids
Word Problem 1. What is the unknown edge of each of the cuboids below?
a) Volume = 600 cm3
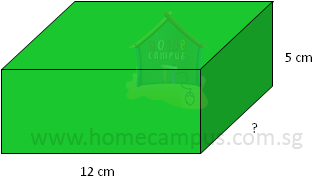

Volume = Length × Breadth × Height
600 = 12 × Breadth × 5
Breadth =
= 10 cm
600 = 12 × Breadth × 5
Breadth =
| 600 |
| 12 x 5 |
= 10 cm
b) Volume = 4500 cm3
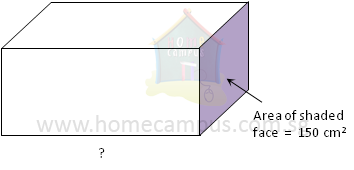

Volume = Length × (Breadth × Height)
= Length × (Area of shaded face)
4500 = Length × 150
Length =
= 30 cm
= Length × (Area of shaded face)
4500 = Length × 150
Length =
| 4500 |
| 150 |
= 30 cm
c) Volume = 6750 cm3


Volume = Area of base × Height
6750 cm3 = 270 cm2 × Height
Height =
= 25 cm
6750 cm3 = 270 cm2 × Height
Height =
| 6750 |
| 270 |
= 25 cm
Word Problem 2: The volume of the Rubik's cube below is 216 cm3. What is the length of one edge of the cube?

The symbol ∛ stands for cube root.
∛(216) is read as the cube root of 216.
6 × 6 × 6 = 216
So, ∛(216) = 6
∛(216) is read as the cube root of 216.
6 × 6 × 6 = 216
So, ∛(216) = 6
Length = ∛(216)
= 6 cm
The length of one edge of the Rubik's cube is 6 cm.
= 6 cm
The length of one edge of the Rubik's cube is 6 cm.
Word Problem 3: A rectangular container with a base area of 200 cm2 is filled with water to a height of 15 cm. If the container has a height of 20 cm, how much water (in litres) should be added to it to fill it completely?
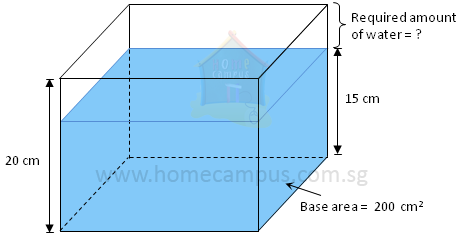
Capacity of container = Base area × Height of container
= 200 cm2 × 20 cm
= 4000 cm3
= 4 litres
= 200 cm2 × 20 cm
= 4000 cm3
= 4 litres
Volume of water = Base area × Height of water level
= 200 cm2 × 15 cm
= 3000 cm3
= 3 litres
= 200 cm2 × 15 cm
= 3000 cm3
= 3 litres
4 litres − 3 litres = 1 litre
1 litre water should be added to the container to fill it completely.
Word Problem 4: Josh built a rectangular cardboard box 18 cm high with a square base and a volume of 2178 cm3. Then he realized he did not need a box that large, so, he chopped off the height of the box reducing its volume to 1331 cm3. Was the new box cubical?
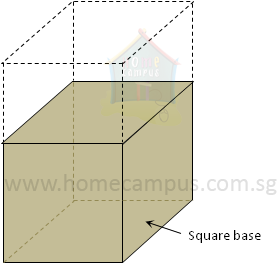
Square base means Length = Breadth
Volume = (Length × Breadth) × Height
= Base area × Height
= Base area × Height
Base area =
= 121 cm2
| 2178 |
| 18 |
= 121 cm2
The symbol √ stands for square root.
11 × 11 = 121
So, √121 = 11
Length × Length = 121 cm2
Length = √(121)
= 11 cm
Length = √(121)
= 11 cm
Now,
1331 cm3 = 11 cm × 11 cm × new height
New height =
= 11 cm
1331 cm3 = 11 cm × 11 cm × new height
New height =
| 1331 |
| 11 x 11 |
= 11 cm
Yes, the new box was cubical (as the length, width and height are all same).
Word Problem 5: A rectangular juice dispenser has a base area of 450 cm2 and a height of 25 cm. Gale adds syrup and water in the ratio 1 : 3 to the dispenser to make a beverage. If he uses 6.75 litres of water, what percentage of the dispenser will be filled when the beverage is made?
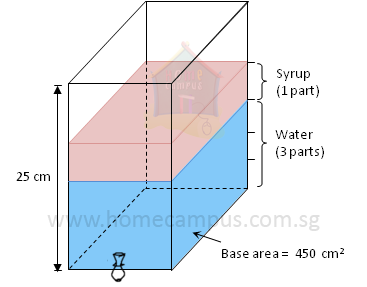
Capacity of dispenser = Base area × Height of dispenser
= 450 cm2 × 25 cm
= 11250 cm3
= 450 cm2 × 25 cm
= 11250 cm3
Syrup : Water = 1 : 3
Volume of water = 6.75 litres
Volume of syrup =
× 6.75 litres
= 2.25 litres
Volume of syrup =
| 1 |
| 3 |
= 2.25 litres
Total volume of beverage = 6.75 litres + 2.25 litres
= 9 litres
= 9000 cm3
= 9 litres
= 9000 cm3
| 9000 |
| 11250 |
80% of the dispenser will be filled when the beverage is made.
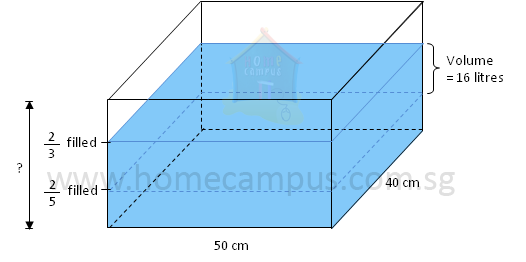
Word Problem 6: A rectangular aquarium is
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
So,
of the capacity of the aquarium = 16 litres
× the capacity of the aquarium = 16 litres
| 4 |
| 15 |
| 4 |
| 15 |
Then,
Capacity of the aquarium = 16 litres ÷
= 16 litres ×
= 60 litres
= 6000 cm3
Capacity of the aquarium = 16 litres ÷
| 4 |
| 15 |
= 16 litres ×
| 15 |
| 4 |
= 60 litres
= 6000 cm3
Therefore,
Height of the aquarium =
= 30 cm
The height of the aquarium is 30 cm.
Height of the aquarium =
| 60000 |
| 50 x 40 |
= 30 cm
The height of the aquarium is 30 cm.
Word Problem 7: The water level in a rectangular tank 65 cm long and 45 cm wide is 14 cm. It will take another 58.5 litres of water to fill the tank to its brim. Find the height of the tank.
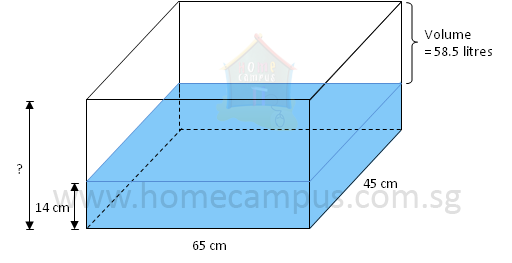
Volume of water in the tank = 65 cm × 45 cm × 14 cm
= 40950 cm3
= 40.95 litres
= 40950 cm3
= 40.95 litres
Capacity of the tank = 40.95 litres + 58.5 litres
= 99.45 litres
= 99450 cm3
= 99.45 litres
= 99450 cm3
Height of the tank =
= 34 cm
The height of the tank is 34 cm.
| 99450 |
| 65 x 45 |
= 34 cm
The height of the tank is 34 cm.
Word Problem 8: Containers A (6 cm, 5cm, 4cm), B (5 cm, 4 cm, 3 cm) and C (3 cm, 3 cm, 2 cm) are three rectangular containers. At first, Container A is filled with water to its brim while containers B and C are empty. Next, some water from Container A is poured into containers B and C so that Container B is completely full while Container C is half full. Find the height of the water left in Container A.
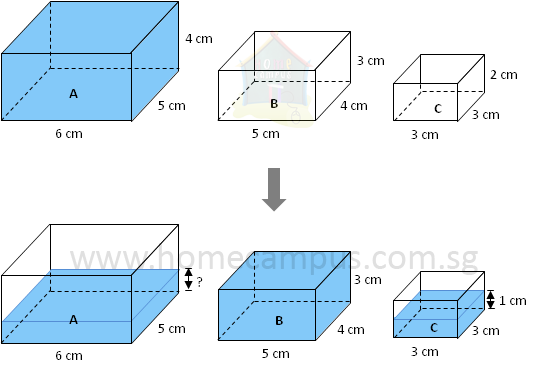
Before
Volume of water in container A = 6 cm × 5 cm × 4 cm
= 120 cm3
Volume of water in container A = 6 cm × 5 cm × 4 cm
= 120 cm3
After
Volume of water in container B = 5 cm × 4 cm × 3 cm
= 60 cm3
Volume of water in container C = 3 cm × 3 cm × 1 cm
= 9 cm3
Volume of water in container B = 5 cm × 4 cm × 3 cm
= 60 cm3
Volume of water in container C = 3 cm × 3 cm × 1 cm
= 9 cm3
Volume of water left in container A = 120 cm3 − 60 cm3 − 9 cm3
= 51 cm3
= 51 cm3
Height of water left in container A =
= 1.7 cm
The height of the water left in Container A is 1.7 cm.
| 51 |
| 6 x 5 |
= 1.7 cm
The height of the water left in Container A is 1.7 cm.
Word Problem 9: A rectangular vase with a square base and 25 cm height is filled with water to its maximum capacity of 1.6 litres. Shelly puts some marbles into the vase causing 235 ml of water to spill. Then she removes all the marbles from the vase causing a further spillage of 85 ml of water. What is the height of the water level in the vase now?
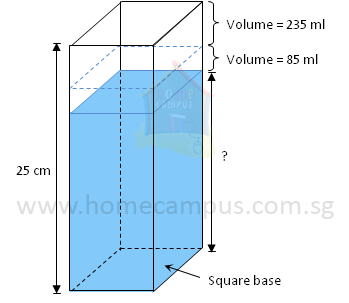
Before the marbles are added to the vase
Volume of water in vase = 1.6 litres
= 1600 cm3
Volume of water in vase = 1.6 litres
= 1600 cm3
Base area of vase =
= 64 cm2
| 1600 |
| 25 |
= 64 cm2
1.6 litres = 1600 ml
After the marbles are added to the vase
Volume of water in vase = 1600 ml − 235 ml
= 1365 ml
Volume of water in vase = 1600 ml − 235 ml
= 1365 ml
After the marbles are removed from the vase
Volume of water in vase = 1365 ml − 85 ml
= 1280 ml
= 1280 cm3
Volume of water in vase = 1365 ml − 85 ml
= 1280 ml
= 1280 cm3
Height of the water level =
=
= 20 cm
The height of the water level in the vase is 20 cm now.
| Volume |
| Base Area |
=
| 1280 |
| 64 |
= 20 cm
The height of the water level in the vase is 20 cm now.
Word Problem 10: An empty rectangular bath tub 150 cm long, 60 cm wide and 50 cm high is being filled with water from a tap at a rate of 30 litres per minute. The tap is turned off after 12 minutes. Water is then drained out of the tub at a rate of 18 litres per minute. What would be the drop in the water level (measured in cm) 6 mintues later?
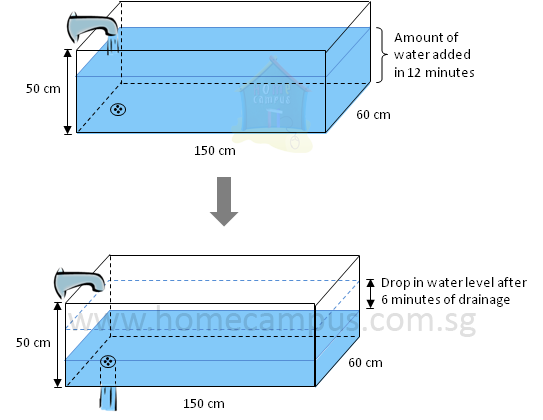
Amount of water added to tub in 1 minute = 30 litres
= Amount of water added to tub in 12 minutes = 30 litres × 12
= 360 litres
= 360000 cm3
= Amount of water added to tub in 12 minutes = 30 litres × 12
= 360 litres
= 360000 cm3
Height of the water level in tub at first =
= 40 cm
| 360000 |
| 150 x 60 |
= 40 cm
Amount of water drained out of tub in 1 minute = 18 litres
Amount of water drained out of tub in 6 minutes = 18 litres × 6
= 108 litres
= 108000 cm3
Amount of water drained out of tub in 6 minutes = 18 litres × 6
= 108 litres
= 108000 cm3
Amount of water left in tub = 360000 cm3 − 108000 cm3
= 252000 cm3
= 252000 cm3
Height of the water level in tub 6 minutes later =
= 28 cm
| 252000 |
| 150 x 60 |
= 28 cm
Difference in heights = 40 cm − 28 cm
= 12 cm
The drop in the water level 6 minutes later would be 12 cm.
= 12 cm
The drop in the water level 6 minutes later would be 12 cm.
Word Problem 11: At 9 am, Kate turned on the supply tap which dispensed water at a rate of 3 litres per minute to fill an empty rectangular container. At the same time, water began leaking out of the container at a rate of 0.5 litres per minute through its faulty tap. Kate turned off the supply tap when the container was filled to its capacity. Given that the container measured 20 cm by 15 cm by 25 cm, at what time was the container completely empty again?
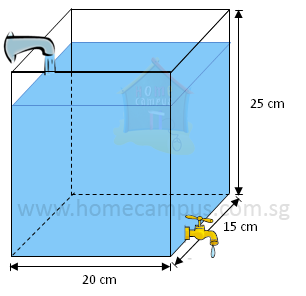
Volume of container = 20 cm × 15 cm × 25 cm
= 7500 cm3
= 7.5 litres
= 7500 cm3
= 7.5 litres
While the supply tap is turned on
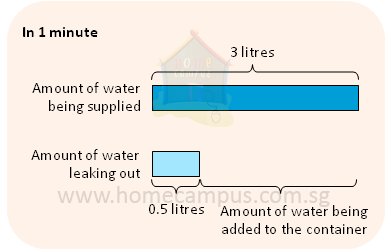

Amount of water being added to the container in 1 minute
= amount of water being supplied − amount of water leaking out
= 3 litres − 0.5 litres
= 2.5 litres
= amount of water being supplied − amount of water leaking out
= 3 litres − 0.5 litres
= 2.5 litres
Time taken to fill the container completely
=
= 3 minutes
3 minutes after 9 am is 9:03 am.
At 9:03 am, the container was filled to its capacity.
=
| 7.5 |
| 2.5 |
= 3 minutes
3 minutes after 9 am is 9:03 am.
At 9:03 am, the container was filled to its capacity.
When the supply tap is turned off
Amount of water leaking out of the container in 1 minute
= 0.5 litres
Amount of water leaking out of the container in 1 minute
= 0.5 litres
Time taken to empty the container completely
=
= 15 minutes
15 minutes after 9:03 am is 9:18 am.
At 9:18 am, the container was completely empty again.
=
| 7.5 |
| 0.5 |
= 15 minutes
15 minutes after 9:03 am is 9:18 am.
At 9:18 am, the container was completely empty again.